2 KAKO RADI RAČUNAR

2.1.1 Šta je binarni zapis?

Elektronska kola od kojih je sagra?en računar mogu biti u jednom od dva radna stanja. Stanje uključeno , kada kroz kolo protiče struja, predstavlja se cifrom jedan (1). Stanje isključeno , kada nema proticanja struje, predstavlja se cifrom nula (0). Pošto su nam na raspolaganju samo dve cifre, 0 i 1, svaki podatak i instrukcija koji se unose u računar moraju biti predstavljeni kao zapis sastavljen od nula i jedinica. U matematici se brojni sistem sastavljen od ove dve cifre naziva binarni brojni sistem. Otuda se i zapis sastavljen od nula i jedinica naziva binarni zapis. Za podatke i instrukcije predstavljene pomoću 0 i 1 kažemo da su binarno predstavljeni, a svaka nula i jedinica naziva se bit.

Šta se sve može predstaviti u binarnom zapisu?

U binarnom zapisu mogu se predstaviti:

• Brojevi: celi i decimalni, veliki i mali, pozitivni i negativni
• Slova: velika i mala slova abecede i interpunkcijski znaci (tačka, zapeta, upitnik itd.)
• Matematički znaci (+, -, =, <, > i dr.), specijalni znaci (@, #, ! i sl.)
• Programske instrukcije
• Kontrolni kodovi: pomeranje kursora, brisanje ekrana...
• Slike i grafički prikazi
• Zvuk: govor, muzika
• Adrese: memorijske lokacije na koje se smeštaju podaci i instrukcije.

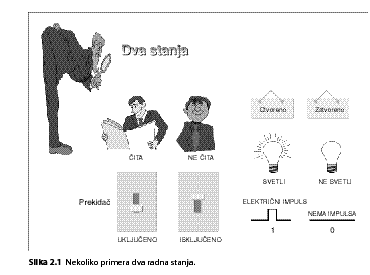
Svaki od ovih oblika predstavlja se jedinstvenim zapisom sastavljenim od 0 i 1. Načini kako se to radi opisani su u ovom poglavlju. Važno je da ih razumete, jer ćete tako shvatiti princip rada računara.

2.1.2 Binarna reč

Koristeći samo cifre 0 i 1, to jest dva bita, možemo napisati četiri zapisa:

0

0

0

1

1

0

1

1

Ukoliko koristimo tri bita, možemo ostvariti osam kombinacija:

0	0	0		1	0	0
0	0	1		1	0	1
0	1	0		1	1	0
0	1	1		1	1	1

Ako bismo poželeli da svaku od sedam duginih boja zapišemo binarno korišćenjem tri bita, to bismo uradili na sledeći način:

Dugina boja	Binarni zapis
Crvena	000
Narandžasta	001
Æuta	010
Zelena	011
Plava	100
Indigo plava	101
Ljubičasta	110

Ukoliko bismo hteli da spektar preciznije opišemo, na primer s deset boja, ne bi nam bila dovoljna tri bita nego četiri da bismo ostvarili potreban broj binarnih zapisa, tako da svaka od deset boja ima svoj kôd.

Ovo je važan zaključak iz koga izvlačimo pouku: za predstavljanje većeg broja različitih podataka neophodan je veći broj bitova u kodu, tj. zapisu. Veza izme?u broja mogućih zapisa i broja bitova definisana je sledećim jednostavnim matematičkim izrazom:

Broj različitih zapisa = 2n

gde je:

n - broj bitova u zapisu.

Iz jednačine sledi da se sa četiri bita može napisati 24 tj. 16 različitih zapisa; sa osam bitova 256 zapisa itd.

Svaki zapis nula i jedinica naziva se kôd. Grupa od osam bitova pore?ana u binarnom zapisu naziva se bajt. Videli smo da se sa osam bitova može ostvariti 256 zapisa. Svaki od tih zapisa može se koristiti za predstavljanje jednog broja, slova abecede ili nekog znaka. Na primer:

• Za slovo A može se koristiti sledeći zapis:

0

1

0

0

0

0

0

1

• Broj 7 može se predstaviti sa:

0

0

1

1

0

1

1

1

• Znak ? može se predstaviti kao:

0

0

1

1

1

1

1

1

Kodovi, odnosno binarni zapisi, smeštaju se na odre?ena mesta, nazovimo ih "kućice". Da bi se tačno znalo gde su kodovi smešteni, "kućice" imaju adresu. U stručnoj terminologiji "kućice" se nazivaju lokacije ili područja (pogledajte sliku 1.11) i nalaze se u memoriji računara.

Sve nule i jedinice na jednoj lokaciji nazivaju se binarna reč . Reč može biti dužine osam bitova, dakle iste dužine kao i bajt, ili 16, 24, 32, 48, 64, 128 ili 256 bitova.

Znaci (ili karakteri) jesu ono što se vidi na tastaturi računara: slova se nazivaju alfabetski znaci ; brojevi od 0 do 9 su numerički znaci, a simboli kao što su #, %, @ ili $ jesu specijalni znaci.

Kada pritisnemo bilo koji taster na tastaturi, u računar se prenese odgovarajuća poruka u obliku zapisa sastavljenog od nula i jedinica. Svaki znak na tastaturi ima svoj binarni zapis ili kôd. Najšire prihvaćen me?unarodni kodni standard je takozvani ASCII kôd. U tabeli 2.1. je pregled ASCII koda. Primetićete da ovaj kôd koristi sedam bitova. Bitovima ASCII koda se s leve strane dopisuje osmi bit da bi ukupan broj jedinica i nula bio paran. Dopisan bit naziva se bit za proveru parnosti. Dakle, u toku obrade na računaru postoji svih osam bitova.

2.1.3 Instrukcije

Računar nije u stanju da obra?uje podatke sve dok mu se ne saopšti šta da radi s njima - neophodno mu je uputstvo po kome će ih obraditi. U tu svrhu mu se u obliku programa daju instrukcije po kojima će postupati u toku obrade podataka. Za pisanje programa, koriste se programski jezici (detaljnije o njima u odeljku 4.2); oni su nama bliski i razumljivi, ali ne i računaru. Zato instrukcije napisane na nekom od programskih jezika treba prevesti, odnosno kodirati na jezik koji računar razume, a to je mašinski kôd. Da bi računar "razumeo" naše zahteve za obradu podataka, treba da zna:

2.1.4 Decimalni i binarni brojevi

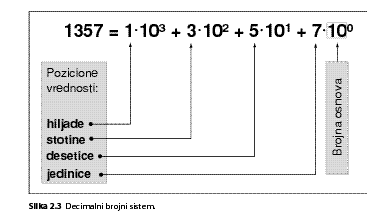
U svakodnevnoj upotrebi su brojevi decimalnog brojnog sistema. To su brojevi čija je brojna osnova 10, a zapisuju se ciframa: 1, 2, 3, 4, 5, 6, 7, 8, 9 i 0. Osim deset cifara, odlika ovog brojnog sistema je da je pozicioni, što znači da svako mesto u zapisu jednog broja pripada klasi jedinica, desetica, stotina, hiljada itd. Primer poziciono raščlanjenog broja 1357 nalazi se na slici 2.3.

Objašnjenja zašto koristimo baš decimalni brojni sistem ima više, od mišljenja da je on racionalan i praktičan za upotrebu do tvrdnje da je čovek davno počeo da ga koristi zato što ima deset prstiju na rukama. Neke stare civilizacije koristile su druge brojne sisteme. Tako su npr. Vavilonci za računanje koristili brojni sistem sa osnovom 60, a neki drugi narodi sa osnovom 20 (verovatno su se pri računanju služili i prstima na nogama). Iz ovoga možemo zaključiti da osnova brojnog sistema ne mora biti 10.

Pošto računar "razume" samo cifre 0 i 1, razmotrimo da li se sa ove dve cifre, tj. s brojnom osnovom 2, može zapisati bilo koji broj korišćenjem pozicionog principa kao u decimalnom brojnom sistemu. Uzmimo za primer broj 19 (pogledajte sliku 2.4).

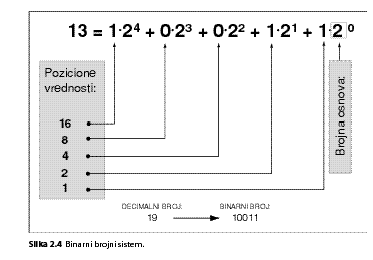
U brojevima sa osnovom 2, tj. u binarnom brojnom sistemu , prva cifra s desne strane označava broj "jedinica", sledeća broj "dvojki", zatim "četvorki", "osmica" itd. Naš primer, broj 19, predstavljen u binarnom brojnom sistemu ima oblik 10011. Kao što smo ovaj broj predstavili u binarnom obliku, tako i bilo koji drugi decimalni broj možemo predstaviti pomoću 0 i 1. Binarni brojevi imaju pozicione vrednosti: 1, 2, 4, 8, 16, 32, 64, 128 itd.

Pošto svakodnevno koristimo brojeve u decimalnom zapisu i u tom obliku ih saopštavamo računaru, a centralni procesor "razume" samo binarne brojeve 0 i 1, računaru se mora omogućiti da pretvara brojeve iz jedne brojne osnove u drugu i obrnuto.

2.1.5 Računanje s binarnim brojevima

Prilikom sabiranja binarnih brojeva koristi se isto poziciono pravilo kao pri sabiranju decimalnih brojeva: me?usobno se sabiraju cifre istih pozicija u brojevima, tj. jedinice s jedinicama, desetice s deseticama, stotine sa stotinama itd. U binarnom brojnom sistemu to znači da se me?usobno sabiraju cifre na pozicijama 1, 2, 4, 8, 16, 32 itd.

Osim ovog, postoje još četiri pravila za sabiranje dve binarne cifre. To su:

Cifre Zbir Prenos

0 + 0 = 0 0

0 + 1 = 1 0

1 + 0 = 1 0

1 + 1 = 0 1

Primera radi, saberimo decimalne brojeve 10 i 9, čiji su binarni zapisi 01010 i 01001.

10 → 01010

+ 9 → + 01001

19 10011

Računari mogu da obavljaju sve vrste aritmetičkih operacija: sabiranje, oduzimanje, množenje i deljenje. Oni obavljaju i vrlo složena izračunavanja i proračune, ali je osnova svih izračunavanja operacija sabiranja. Jedan broj se može oduzeti od drugog tako što će se pretvoriti u negativan i potom sabrati:

7 - 5 = 7 + (-5) = 2

Većina računara koristi ovaj princip za oduzimanje brojeva. Za to se koristi operacija komplementiranja (svaka jedinica se pretvara u nulu a nula u jedinicu). Množenje se obavlja uzastopnim sabiranjem:

3 × 7 = 7 + 7 + 7 = 21

Deljenje se obavlja uzastopnim oduzimanjem.

2.1.6 Skraćeni zapis binarnog koda

Dugački nizovi nula i jedinica, kao zapisi većih ili velikih brojeva u binarnom sistemu, teško se pamte. Osim toga, ovakvi zapisi zahtevaju mnogo koncentracije i vremena za ispisivanje. Iz tih razloga, često se koristi skraćeni zapis binarnog zapisa, čime se on čini prihvatljivijim. U tu svrhu koriste se heksadecimalni i oktalni zapisi.

Kao što smo utvrdili, mikroprocesor prihvata reč dužine 8 bita. Ove reči mogu biti podeljene u dve grupe po 4 bita, npr. 0001 i 1110. Obe ove četvorobitne grupe mogu biti ure?ene na 16 načina, što znači da se njihovi kraći zapisi mogu ostvariti korišćenjem brojeva sa osnovom 16, to jest korišćenjem heksadecimalnih brojeva. Za označavanje decimalnih brojeva 10, 11, 12, 13, 14, 15 i 16 u heksadecimalnom sistemu koriste se slova A, B, C, D, E i F, što se vidi u tabeli 2.2.

Heksadecimalni kodovi se najčešće koriste u računarima sa 8-bitnim i 16-bitnim binarnim kodom.

U računarima koji rade s dužim rečima koriste se i neki drugi tipovi skraćenih zapisa, kao što je npr. oktalni brojni sistem.

Oktalni brojni sistem koristi samo osam cifara: 0, 1, 2, 3, 4, 5, 6 i 7.

Tabela 2.2 Heksadecimalni zapis

Binarni kodovi (4 bita)	Heksadecimalni zapis
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Ključno!

Svaki zapis u računaru predstavlja se nulom i jedinicom. Podaci predstavljeni pomoću nula i jedinica predstavljeni su binarno. Niz nula i jedinica smeštenih na jednoj lokaciji u memoriji računara naziva se binarna reč. Cifra 0 ili 1 u binarnom zapisu naziva se bit. Grupa od osam bitova pore?anih u binarnom zapisu naziva se bajt. Znakovni kodovi koriste binarne zapise koji predstavljaju slova abecede, brojeve, znake interpunkcije, specijalne znake itd. Instrukcije koje računar treba da izvrši i memorijske adrese na koje se smeštaju te instrukcije tako?e su date u obliku binarnog zapisa, tj. binarnog koda. Budući da elektronska kola u računaru mogu biti u samo jednom od dva moguća stanja, znači da računari rade s binarnim brojevima. Binarni brojni sistem je pozicioni baš kao i decimalni brojni sistem. Decimalni brojevi se mogu prevesti u binarne brojeve i obrnuto, poštujući odre?ena pravila. Tim pravilima se pokoravaju i računari. Računar "zna" da razlikuje cele, realne, pozitivne i negativne brojeve. Na osnovu odre?enih pravila računar sabira, oduzima, množi, deli i obavlja složena izračunavanja. Oktalni i heksadecimalni brojevi koriste se za skraćeno zapisivanje dugačkih binarnih brojeva.

2.2.1 Računarska logika

U računaru se bitovi predstavljaju električnim impulsima. Električni impuls predstavlja 1, a stanje bez impulsa predstavlja 0. Impulsi se stvaraju tako što se struja provodi kroz elektronska kola računara preko elektronskih prekidača , ili kako se češće nazivaju, logičkih kola .

Logičko kolo može biti otvoreno i tada propuštanjem struje stvara impuls ili impulse, ili pak zatvoreno, kada zaustavlja proticanje struje i stvaranje impulsa. Logičko kolo nema mehaničkih pokretnih delova kao što ih imaju npr. prekidači za struju po kućama; otuda, iako funkcioniše slično prekidaču, nema zvuka sličnog škljocanju.

U računaru postoji mnogo me?usobno povezanih logičkih kola, što omogućava da se impulsi upućuju u raznim pravcima unutar ovih veza (puteva) i kombinuju po odre?enim logičkim pravilima.

U logičko kolo ulazi odre?ena kombinacija impulsa a izlazi druga, tako?e odre?ena kombinacija. Ovo kombinovanje ulaznih impulsa da bi se dobio odre?eni izlaz impulsa naziva se računarska logika .

Kombinovanje impulsa po utvr?enim logičkim pravilima jeste drugi zadatak logičkih kola.

Dakle, logička kola stvaranjem ili prekidanjem impulsa fizički stvaraju bitove 1 i 0, a kombinovanjem impulsa po logičkim pravilima omogućavaju primenu binarnog brojnog sistema, o kome je bilo reči u prethodnom odeljku.

2.2.2 Osnovna logička kola

NE-kolo: Ovo je najjednostavnije logičko kolo. Njegova logika je ovakva: ako na ulazu primi impuls (bit 1), na izlazu nema impulsa (bit 0); ukoliko na ulazu nema impulsa (bit 0), na izlazu se javi impuls (bit 1).

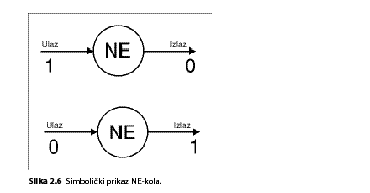
Na slici 2.6. simbolično je predstavljeno NE-kolo, u kome se signal s ulaza uvek promeni na izlazu. To se može prikazati i jednostavnom tabelom, takozvanom tabelom istinitosti ili tabelom operacija .

Tabela 2.3 Tabela istinitosti NE-kola

Ulaz	Izlaz
1	0
0	1

I-kolo: Ovo osnovno logičko kolo nešto je složenije od NE-kola. Ono u principu ima dva ulaza i jedan izlaz. Kada je na oba ulaza 1 i izlaz je 1. U svim drugim kombinacijama signala na oba ulaza, izlaz je uvek 0. Na slici 2.7. simbolički je predstavljeno I-kolo.

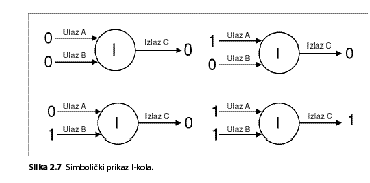
U tabeli istinitosti (tabela 2.4) prikazane su sve kombinacije ulaznih i izlaznog signala.

Tabela 2.4 Tabela istinitosti I-kola

Ulazi		Izlaz
A	B	C = A i B
0	0	0
1	0	0
0	1	0
1	1	1

I-kolo može imati više od dva ulaza, ali i tada važi isto pravilo: izlaz je 1 samo ako je na svim ulazima 1.

ILI-kolo: Ovo kolo, slično I-kolu, može imati dva ili više ulaza i samo jedan izlaz. Kolo daje 1 na izlazu ako je bilo koji od ulaza 1 ili su oba 1. U tabeli istinitosti (tabela 2.5) prikazane su sve kombinacije nula i jedinica ovoga kola.

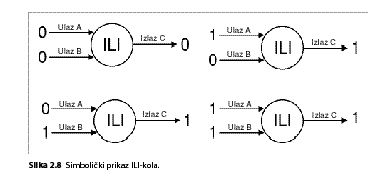
U ILI-kolu izlaz je 0 samo ako su oba ulaza 0.

Tabela 2.5 Tabela istinitosti ILI-kola

Ulazi		Izlaz
A	B	C = A ili B
0	0	0
1	0	1
0	1	1
1	1	1

Ako ILI-kolo ima više od dva ulaza, važi isto pravilo: izlaz je 0 samo ako su svi ulazi 0.

Kola NE, I i ILI nisu jedina logička kola; postoje i druga, na primer: NI, NILI (NE--ILI) i EKSKLUZIVNO ILI.

2.2.3 Logički sklop

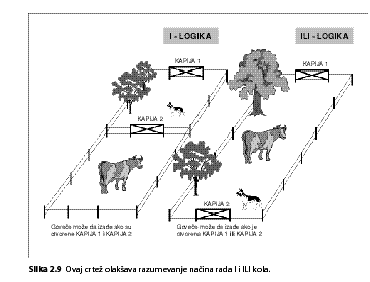
Logička kola (NE, I, ILI) mogu se me?usobno povezati u logički sklop ili logičku mrežu . Od tri osnovna logička kola mogu se formirati jednostavni ili složeni logički sklopovi. U stvari, korišćenjem ova tri osnovna logička kola mogu se formirati svi računarski logički sklopovi. Logički sklopovi u računaru obavljaju sledeće poslove:

• dekodiranje instrukcija
• prenos podataka i upravljanje tokom podataka s jedne lokacije na drugu
• izračunavanja, npr. sabiranje dva binarna broja
• pore?enje binarnih reči
• memorisanje podataka.

Na slici 2.10 je primer jednostavnog logičkog sklopa za sabiranje, koji se naziva polusabirač .

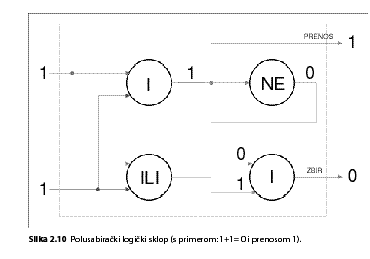
Sami proverite način rada polusabirača na osnovu pravila o sabiranju binarnih brojeva opisanog u odeljku 2.1.4.

Logički sklopovi retko greše prilikom izračunavanja. Me?utim, ponekad se mogu pojaviti neočekivani rezultati. Jedan razlog može biti što se neki razlomci (npr. 2/3 = 0,666666...) ne mogu tačno predstaviti u binarnom obliku. Drugi mogući razlog je prekoračenje: prilikom izračunavanja rezultat može biti toliko velik (tj. imati previše bitova) da ne može stati u za njega predvi?enu memorijsku lokaciju.

Ipak, računari koji mogu da obave veoma složene proračune i ogroman broj izračunavanja konstruisani su tako da greške svedu na minimum. Da je to tačno najbolje govore činjenice o tačnosti računarskih proračuna koji omogućavaju milimetarski precizna spajanja kosmičkih brodova sa vasionskom stanicom u orbiti oko Zemlje.

Ključno!

Logičko kolo propušta ili ne propušta električnu struju i na taj način stvara impuls ili impulse. Tri osnovna logička kola su: NE, I i ILI. Tabela istinitosti prikazuje logiku rada logičkih kola. Kombinovanjem logičkih kola povezanih u jednu celinu formiraju se logički sklopovi. Kombinovanje ulaznih impulsa da bi se dobio odre?eni izlazni impuls naziva se računarska logika. Logička pravila su pravila po kojima se mogu kombinovati impulsi. Logički sklop za sabiranje dve binarne cifre zove se polusabirač. Postoje i druga važna logička kola, kao što su: NI, NILI i EKSKLUZIVNO ILI.